Binary search

The binary search algorithm allows you to efficiently check if the value exists and get there index from an array. It does not need to iterate over the whole array which complexity is O(n) . But thanks to its design it can find the solution in O(log n) time. But the important precondition is fact, that array must be sorted.

The algorithm

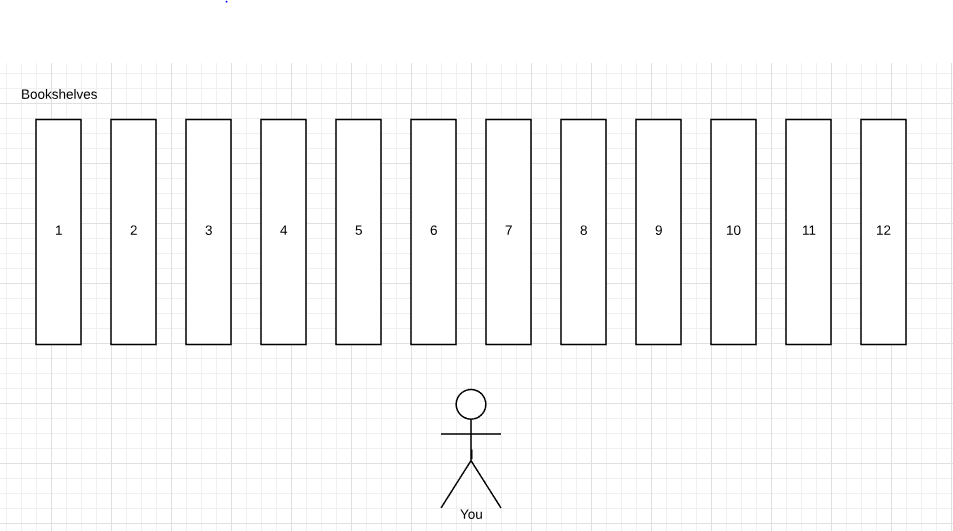
Let’s start with a story, which will help you understand how it works. Imagine you enter first time a big library. You see in front of you 12 bookshelves. Those bookshelves have only number on them and do not have any information about letters. You want to rent a Harry Potter book.

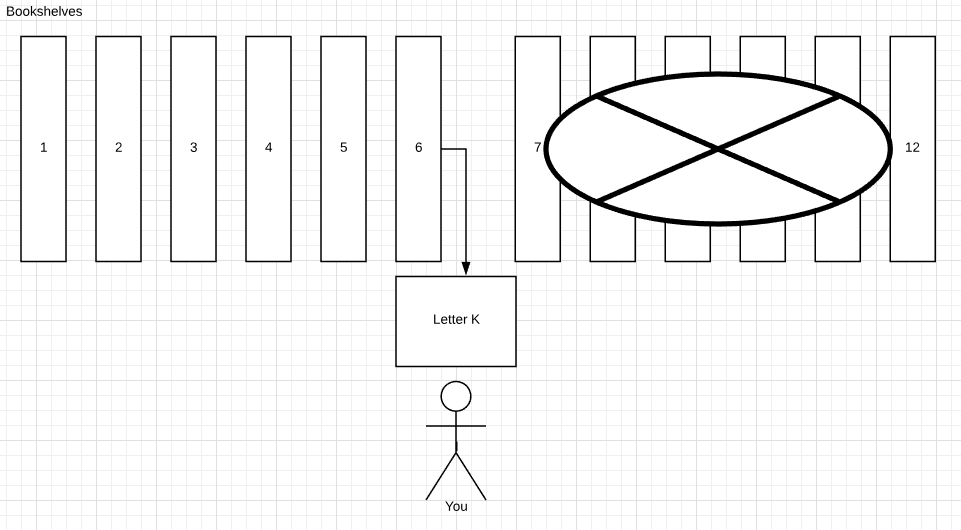
Ok, so there are 26 letters in the alphabet. H is the 7th letter. But you know that the number of books for each letter is not equal. Therefore you decide to check what letter is in the middle. And then you’ll choose either left or right part. At the shelf number 6, you see the letter K.

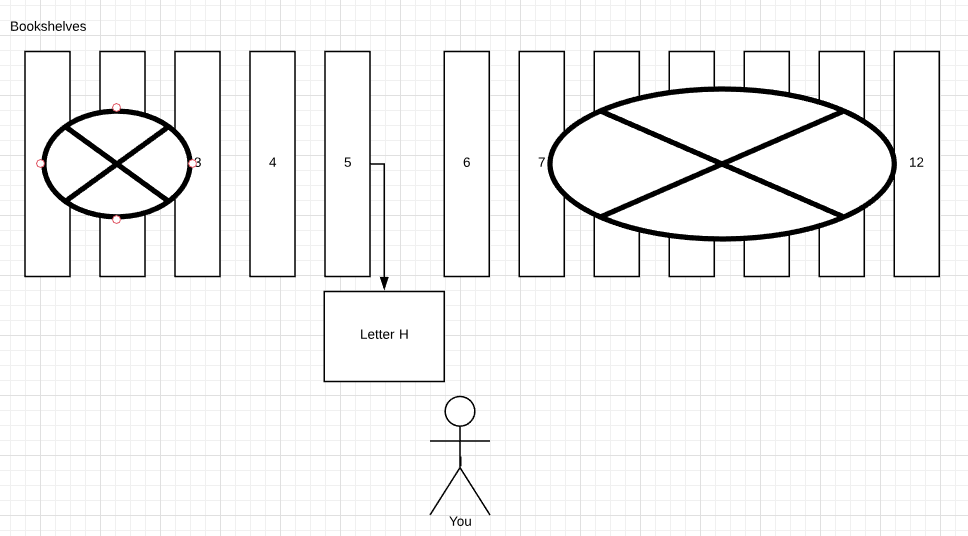
A ha! So you know that there is no way that your Harry Potter book will be in the shelves greater than 6. So where it might be? You decide to check what letter will be between shelves 3 and 4, in the middle of the ‘data’ which is still available. You see the letter E. So there is not possible that your book will be somewhere on the shelves 1-3. You eliminate them. Now you have only shelves 4,5,6. You check the middle one. Shelve number 5. And there it is! Letter H.

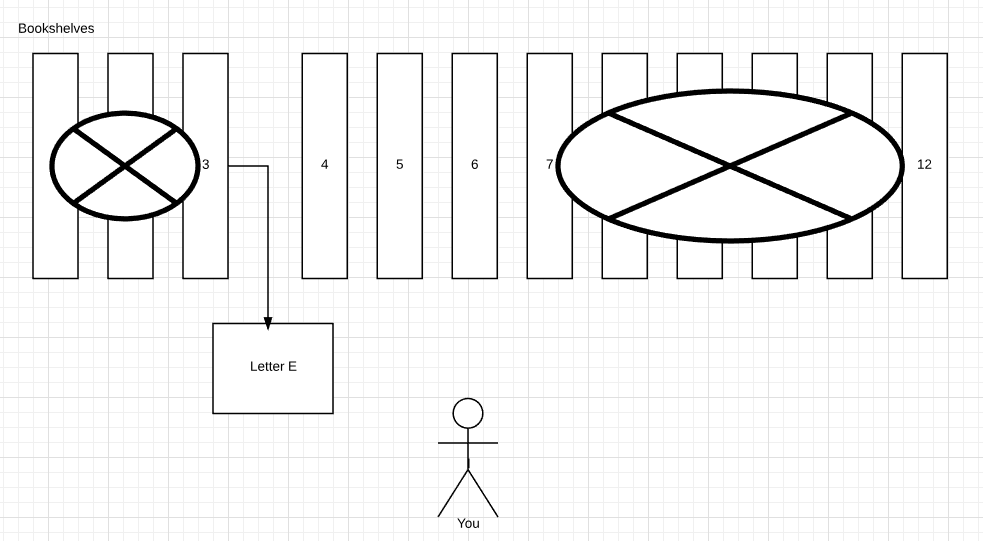
Ok, you see the pattern now? You always cut the data in half, and check what’s in the middle.

Implementation

Let’s represent this problem using code

/* we use charcodes
A = 65
Z = 90

what we are looking for is H
H = 72
*/

const data = Array.from(Array(26), (e, i) => i + 65)
let X = 72

const binarySearch = (data, X) => {
  let left = 0 // first index
  let right = data.length - 1 // last index
  while (left < right) {
    let middle = Math.floor((left + right) / 2)
    if (data[middle] < X) {
      // value is smaller, it must be on 'the right' part of daa
      left = middle + 1
    } else {
      right = middle
    }
  }

  if (data[left] === X) {
    return left
  } else {
    return -1 // not found
  }
}

binarySearch(data, X) // returns 7

It’s allso possible to write this algorithm in recursive manner

const binarySearchRecursive = (data, X, left, right) => {
  if (left > right) {
    return -1
  }

  const middle = Math.floor((left + right) / 2)

  if (data[middle] === X) {
    return middle
  } else if (data[middle] < X) {
    const newLeft = middle + 1
    return binarySearchRecursive(data, X, newLeft, right)
  } else {
    const newRigtht = middle
    return binarySearchRecursive(data, X, left, newRigtht)
  }
}

Remarks

• array must be sorted
• MUCH faster than linear search (remember always looking at the average case scenario)

resources

• Video about binary search
• Wikipedia article